はじめに

AIの運動計画問題は人工知能の分野でも近年、特に注目されている分野です。GoogleのDQNがニューラルネットワークを用いてAtariのゲームを解いたこと（関連記事はこのへんとかこのへんとかこのへんとか）をきっかけとして、AIに複雑な運動計画問題を解かせるということは多くの研究者、技術者たちの興味の対象となっています。しかしながら、DQNは強化学習と呼ばれるテクニックで、強化学習には大量の調整パラメータをどうすればいいのかとか、実際にAIがよい動作をするまでに学習に大変な時間がかかるなど、いまだ解決されていない問題が多くあります。 DATUM STUDIOにも「最近はGoogleがDQN使っててすごい流行ってて！これでAI作ってよ！」というお客様の相談がたびたび舞い込んできます。しかしながらお客様の相談の中には明らかにDQNではなく、従来使われてきた古典的な運動計画問題を適用したほうが、または古典的な手法と組み合わせることで効率的に問題を解くことができるであろうという依頼が少なくありません。 強化学習を用いたアプローチは確かに従来の手法でカバーしきれなかった複雑な問題設定を解くことができますが、決して全ての問題に適した万能手法でないことに注意しなければなりません。簡単な問題設定や、強化学習を使う必要性のない場合などは従来の運動計画手法などを用いた方が導入コストも運用時の計算コストも実際の動作精度も良くなるでしょう。 今回はそれらの観点から数多く存在する運動計画問題の中でも、制御対象のダイナミクスに制限などが少なく、比較的簡易な問題設定である経路生成問題でメジャーに使われているRapidly exploring random tree(RRT)アルゴリズムを紹介します。

RRT

RRTの特徴は以下の通りです。

• 割と高速に探索可能
• 原理が単純で実装が簡単
• 派生型アルゴリズムが数多く存在して改良が楽

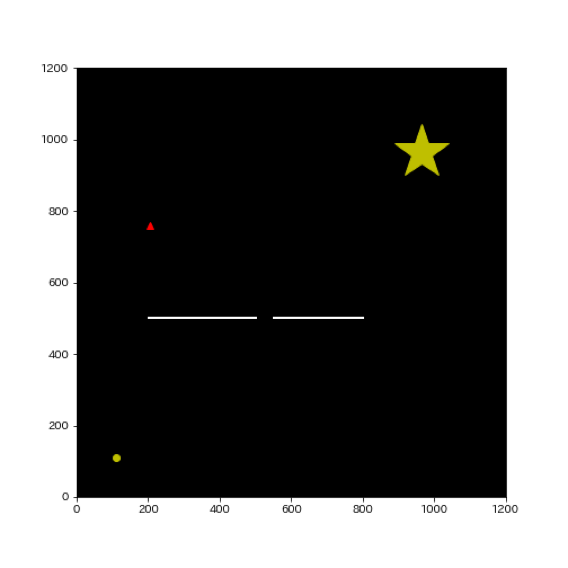
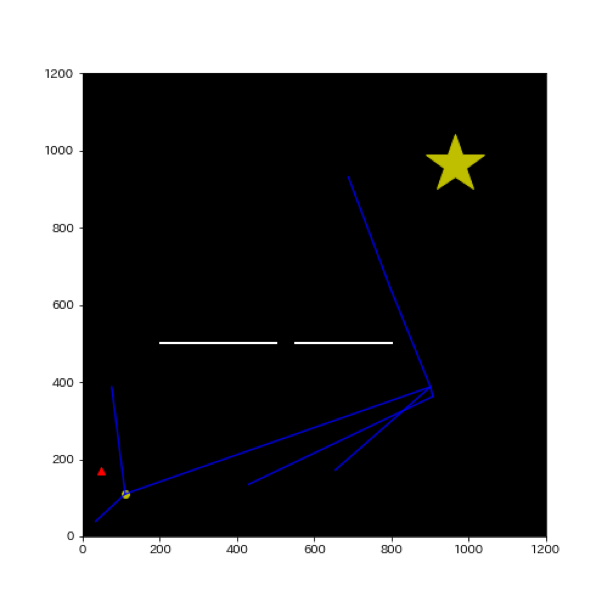
RRTアルゴリズムは経路生成問題の世界でも特にロボット開発の領域で最もメジャーなアルゴリズムです。１９９９年に提案がされた割と新しいアルゴリズムですが、当時のべらぼうに遅いコンピュータでもそれなりに多くの問題に適用することができるアルゴリズムの高速性と、その原理がシンプルで誰でも実装ができたためにポピュラーな手法として広まりました。 RRTは改良をしていない純粋なアルゴリズムでは運動計画問題(motion planning algorithm)ではなく経路探索問題(path planning algorithm)として分類される手法になります。しかしながら経路の引かれ方にロボットのハードウェアの制約（モーター電圧や加速度制限）などを考慮させることで運動計画問題を解くことができるようになります。 動作の解説のために、全方向に動くことが可能な全方向移動ロボットを仮定してアルゴリズムを作成しました。〇がスタート位置で★がゴール位置になります。

1. １：RRTではまずランダムに環境中に点を置きます（ランダム点を▲で表示）

   

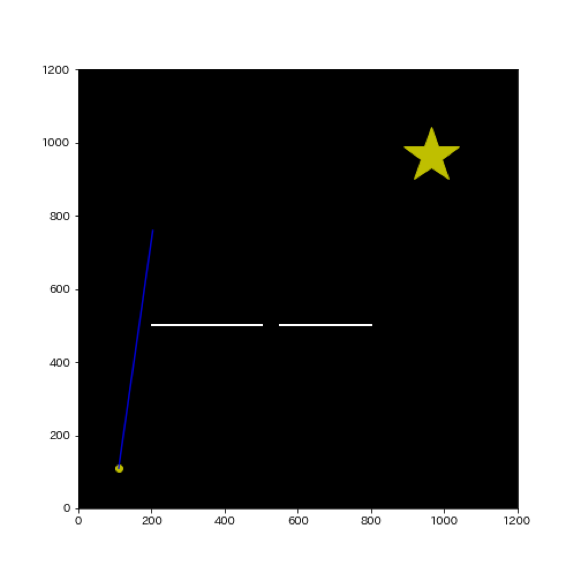
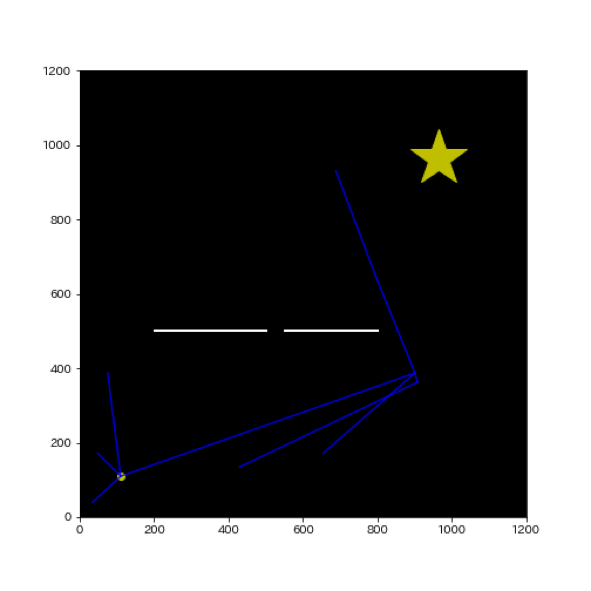
2. ２：そして次に▲に向かって初期点から１ステップで移動可能な量の分まで経路を引きます。この際に障害物があったら、その方向の経路生成は失敗でまたステップ１に戻ります。

   

3. ３：障害物もなく問題なく経路を引くことができた場合はその経路を運動計画を保存する木構造に追加します。
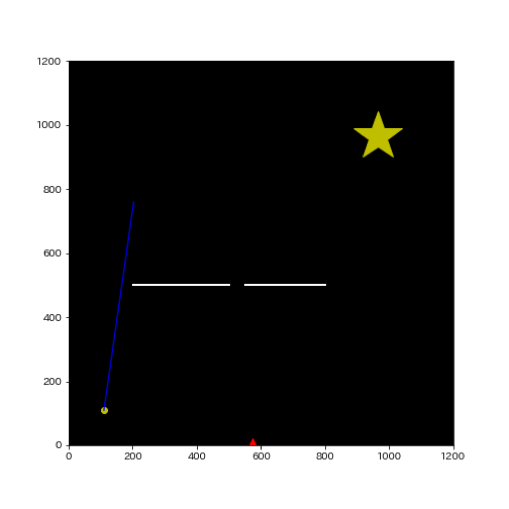
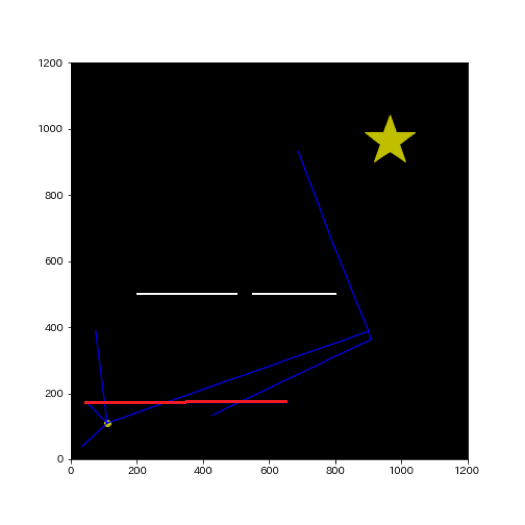
4. ４：木構造に追加をしたら今度は再度ランダムに探索を行います（ランダム点を▲で表示）

   
   

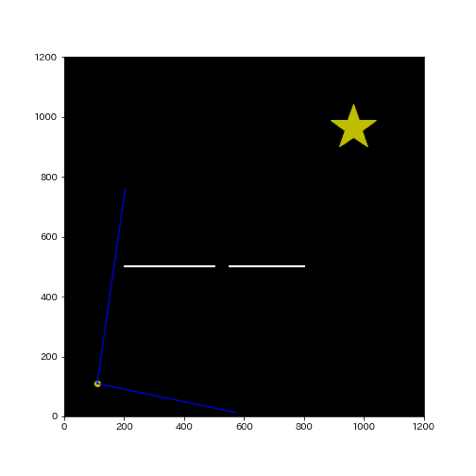
5. ５：次に▲に向かって初期点から１ステップで移動可能な量の分まで経路を引きます。この際に今度は▲に向かって経路を伸ばす原点となる点を初期点ではなく、木構造の中から最も近い経路点の中から選択します。
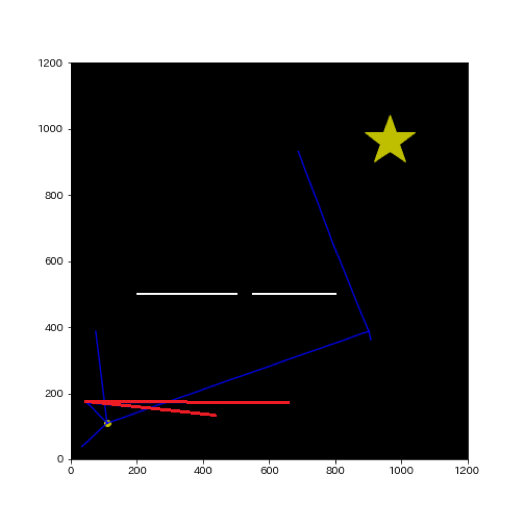
6. ６：障害物もなく問題なく経路を引くことができた場合はその経路を木構造にまた追加してステップ４に戻ります。

これがRRTの全ステップになります。解説のために初期点のみのステップ１、２、３をはさみましたが、実際には初期点も木構造の1つと捉えれば実際のステップは４、５、６のみとなります。わずか３ステップで運動計画問題を解くことができました。全方位移動ロボットではなく、carシステムや多関節ロボットなどを用いた運動計画問題を解く場合にはステップ３、５における移動可能な経路を引くという場所を変更して制約を考慮させることで対応させることができます。 しかしながらRRTには問題があります。それは生成される経路に最適性がないという問題です。最短経路を生成する場合には次に紹介するRRT*アルゴリズムを用いる必要があります。

RRT*

RRT*(RRTstar)の特徴は以下の通りです

• RRTでできなかった最適性の考慮が可能
• RRTと同じく原理が単純で実装が簡単
• 計算コストがRRTの倍程度かかる

RRTアルゴリズムはとにかく単純かつ高速なアルゴリズムとして大流行をしました。しかしながらRRTには問題がありました。それは最適な運動計画が実行できないという問題です。ざっくりとはなんとなく良質な運動をすることができるのですが、決して最適な運動をしないのです。 そこで2010年にS Karamanにより生み出されたのがRRT*になります。

• 論文元：http://roboticsproceedings.org/rss06/p34.pdf

RRT*はRRTを改良して無限回の探索をしたときに最適な運動計画が実行される保障のある最適運動計画用のアルゴリズムになります。 改良した部分としてはRRT*では新しい経路を木構造に追加する際に、もともとあったデータに対して経路を引き直したらよりよい経路が引けるのではないかということを検討します。

1. 1：既に下のような木構造があるとし、まずは通常のRRTと同じく新たに再度ランダムに探索を行います（ランダム点を▲で表示）

   

2. ２：通常のRRTと同じく、木構造の中の最も近いノードと線を結び、間に障害物がなければ新たなノードとして木構造に追加します。

   

3. 3:次に新しく加えられたノードから現在の木構造のノードへの新しい経路を考え、そちらが現在の経路より少ないコストで移動できるならば経路を新しく引き直します。

   

4. ４:経路の引き直しを対象となる近いノード全てに対して考えます

   

以上の４ステップを繰り返しながら経路を探索していきます。探索のたびに既存のノードへの最短パスが計算しなおされることになるので、無限回の探索で必ず最短経路が引かれることが保証されています。ただし、RRT*では計算コストが経路比較のための計算に必要となるため、単純なRRTの倍程度の計算が必要となるのが欠点です。 探索効率の改善に関してはヒューリスティックな手法が数多く知られていますが、中でも次に紹介をするinformed-RRT*は単純障害物のみが存在する環境では非常によく動くアルゴリズムとして知られています。

Informed-RRT*

, 14M Informed-RRT*は極めて単純な仕組みでRRT*における経路最適化の効率化を達成する強力なアルゴリズムです。２０１４年にJonathan D. Gammellに提案され、極めて簡単にRRT*を高速化できることから人気を呼びました。

• 元論文：https://arxiv.org/pdf/1404.2334.pdf

あらゆる環境でよく動くわけではありませんが、最短経路が直線状に近いほどに探索が簡単になる特性は複雑すぎる動作を要求されない現在のロボット界隈にはちょうどよい技術と呼べます。。 Informed-RRT*の基本的なアルゴリズムはまったくRRT*と変わりません。唯一の違いはランダムサンプリングの方法が異なるのみです。 informedRRT*ではまずは通常のRRT*を実行した後、ゴールまでの経路が一つでも見つかったら、その経路長の情報を用いてサンプリングする探索領域を楕円形上に限定します。楕円形上は最短経路長が小さくなるごとに面積が小さくなっていき、無駄な探索領域が省略されることで探索が効率化します。 探索は下のgifのように通常のRRT*と比較して圧倒的に効率化されているのがわかります。