word2vecを使い記事からベクトルへの変換
本記事は新人の視点から理解したword2vecを紹介します。
word2vecのハラワタ(内部モデル)を透視して、各機能やハラワタ間の関係を総括します。本記事の後に、word2vecに関する勉強と研究も続けて、最終的な目的は個人のword2vecモデルを作成します。 2017年6月まで、複数のブログや論文を読んで、お互いに矛盾している箇所があるので、「結局どれが正しいの?」がわかりづらくなっています。読者の理解を助けるため、記事の最後に矛盾と不明なところを総括します。
目次
背景
近年、Deep Learningが急速的に発展されています。特に、2013年から今まで、Deep Learningは画像認識、ビデオ認識領域では大きく発展して、YoutubeのContent ID(著作権者は、動画に含まれるコンテンツと自分の作品が一致するかどうかの判定、2013年)、アリババの顔認識電子決済システム(2015年)など、技術と商業化が同時に展開しています。 筆者は、今年は初めてDeep Learningを知りました。機械学習に関する知識が不足のため、Deep Learningの学習はとても困難でした。しかし最近では、word2vecと出会い、すぐに興味を持ちました。 word2vecは単語をK次元のベクトル空間にマッピングし、Cosine類似度などの手法では、単語間の関連性(文法と文意)を算出するモデルです。
word2vecとは
word2vecは、2013年にopen sourceに効率的に単語を数値ベクトルに変換ツールの一種です。ハラワタはCBOWとSkip-Gramです。
word2vecとDeep Learningの関係
word2vecはDeep Learningの一種と見なすことができます。原因はTomas Mikolov(word2vecの作者)とDeep Learningの関係、もう一つの原因は、word2vecはDeep Learningの構造(入力層、中間層、出力層)を採用しました。 筆者は、word2vecはDeepではないと思います。Output layerの出力はベクトルだから、特徴量として、別のDeep Learningの入力層になることもできます。Tomas MikolovのRNNモデルと比べて、word2vecの出力は再処理の必要があると思います。
word2vecの利点
生データ(raw data)を学習して、生データの単語(重複なし)をK次元のベクトルになり、Cosine類似度、ユークリッド距離などの手法を通して、単語間の類似度は文意類似度を見なします。そのため、word2vecはクラスタリング、同意語計算などは得意です。
関連知識
本節では、既存のWord Vectorを紹介します。
One-hot
今、一つの文「I have an apple. 」があります。句読点除き、単語間にスペースを入れ、前処理を行い、「I have an apple」を取得します。 次に、重複なしの単語はリストに入れ、「‘I’、‘have’、‘an’、‘apple’」を取得します。毎単語に対して、ベクトルを生成し、
| I | [1,0,0,0] |
| have | [0,1,0,0] |
| an | [0,0,1,0] |
| apple | [0,0,0,1] |
このベクトルはOne-hotベクトルと呼ばれます。 One-hotベクトルの特徴は、対応する単語の位置が「1」、その他の位置は全部「0」となります。利点は簡単なことに対し、欠点は同意語間の関連が弱い、n個の単語(重複なし)に対してnの二乗個のデータを計算しなければならないため計算量が重いことです。 同意語間の弱い関連性について、少し説明します。上記の例に、もう一つの文[I have a pen]を追加したら、One-hotベクトルは下記になります。
| I | [1,0,0,0,0,0] |
| have | [0,1,0,0,0,0] |
| an | [0,0,1,0,0,0] |
| apple | [0,0,0,1,0,0] |
| a | [0,0,0,0,1,0] |
| pen | [0,0,0,0,0,1] |
同意語「an」と「a」は各々対応されたベクトル[0,0,1,0,0,0]と[0,0,0,0,1,0]から見ると、相関していると考えるのは困難です。同意語を関連したい時、どうすればいいでしょうか? 記事を続けて読んでください。
分散表示
word2vecは分散表示を採用しました。一つのword vector(ここではモデルではない)は数百の次元があります。例えば、単語「I」の分散表示は[0.93, 0.95, 0.94, 0.21…]のような形になり、単語の全部の要素の重みを一つのベクトルに入れて、一個の単語を表せます。つまり、分散表示は一部の単語(要素)を使って、全部の単語と要素間の関連性が数値になります。
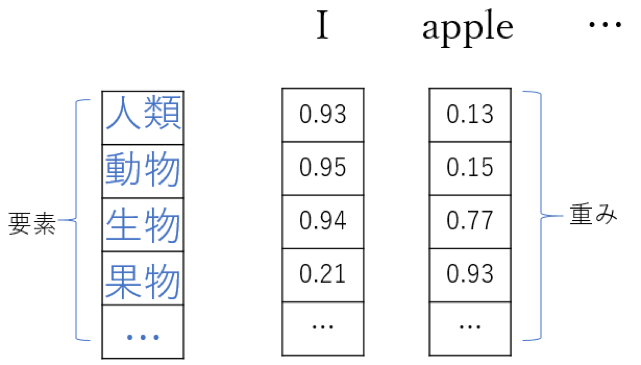
分散表示の主旨は、単語を使い単語を表します(use words to describe other words)。上の例では、「I」という人間を表す単語に対し、要素「人類」との相関性数値が0.93になっています。なお、上の例はAdrian Colyerの技術ブログ「The amazing power of word vectors」を参照しました。例で表示される数値は全部仮のものです。 しかし、上記ブログは次の二つの疑問を答えませんでした。
- 要素の生成方法とどのような要素を入れるのかははっきり説明しませんでした。
- 重みの計算方法は不明です。
CBOW
次に、CBOWを紹介します(筆者は多方面の資料を参照しましたが、資料同士に矛盾するところがあるため、CBOWに関する理解は正しいかどうか分かりません)。 CBOWは三つの層(layer)があります。入力層、中間層、出力層です。 今、文[The recently introduced continuous Skip-gram model is an efficient method for learning high-quality distributed vector representations that capture a large number of precise syntax and semantic word relationships.]があるとします。文上でスライドウィンドウを左から右にスライドします。スライドウィンドウの真ん中位置にいる単語は対象単語と呼びます。真ん中を見るのでスライドウィンドウのサイズは奇数を推奨します(実は対象単語の下記側しか見ない手法もあります)。

次に上記と下記をCBOWに代入します。
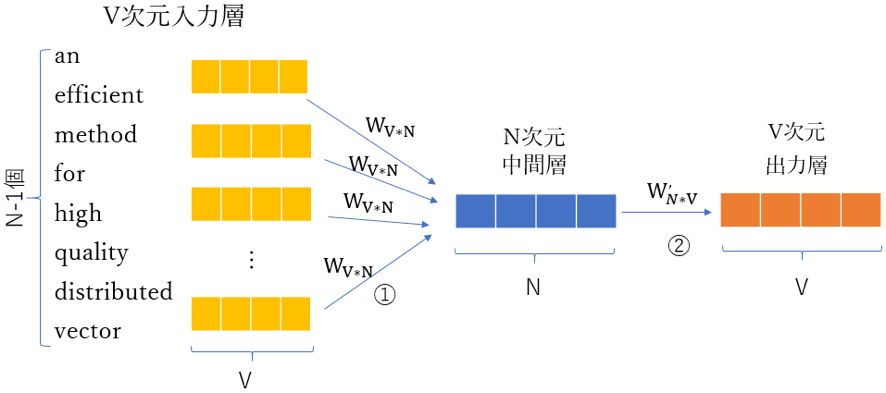
CBOWは入力層、中間層、出力層の構造を採用します。入力層はn-1個のベクトルです。nはスライドウィンドウのサイズです。入力層のベクトルはv次元のベクトルです。なお、vはベクトル中の数値の個数です。 CBOWでは入力層と中間層の間に、重み行列\(W_{V*N}\)があります。V行N列の行列です。CBOWモデルの図中の①です。
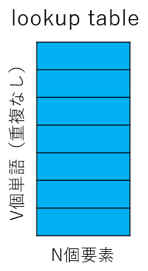
中間層と出力層の間に、重み行列\(W’_{N*V}\)があります。なお、\(W’_{N*V}\)は\(W_{V*N}\)の転置行列というわけではありません。

生データ学習の目的は、出力単語(対象単語)の条件付き確率を最大化することです。上の例では、入力は「’an’、‘efficient’、‘method’、‘for’、‘high’、‘quality’、‘distributed’、‘vector’」で、出力が‘learning’の条件付き確率を最大化します。 Lookup tableを使い、V次元のベクトルはN次元に圧縮されます。一般的にコーパスには単語(重複なし)が数万以上あります。Nは一般的に一千以内とし、疎ベクトルを圧縮し、多次元の行列計算効率を大幅に上昇させます。 中間層を掛け、出力層ベクトル(原文はOutput Vector)を算出できます。更に出力層ベクトルにSoftmax(log linear)関数を通して、結果を算出します。結果は多項分布のパラメーターと見ることができます。
CBOWのまとめ
下の図は一個の入力ベクトルがCBOWに入れて最後の結果を算出するまでの流れです。

入力層は複数のベクトル(原文はInput vector)です。入力層はlookup tableを掛けて、中間層を算出します。中間層の次元はn≤1000。中間層は重み行列を掛けて一時出力層になります。更に結果はSoftmax(log linear)関数を通して処理して、最終結果を取得します。
疑問
- 重み行列どのような手法で取得、算出できるのでしょうか。ブログはこの部分の説明がありません。上の図は仮の数値ですが、コーパスを処理する時に使うlookup tableと重み行列はどのようになっているのでしょうか。コーパスを処理する過程中ではlookup tableと重み行列中の重み数値をどのように更新するのでしょうか。
- 出力層は多項分布ですが、どのような方法で多項分布と単語を関連付けられるのでしょうか。
Skip-Gram
CBOWを逆向きにしたのが、Skip-Gramになります。CBOWの入力層はn-1個のベクトル、出力層は1個のベクトルです。Skip-Gramは逆になり、入力層は1個のベクトル、出力層はn-1個のベクトルです。 下はXin Rongの論文で「word2vec Parameter Learning Explained」採用した一般化されSkip-Gramの図です。
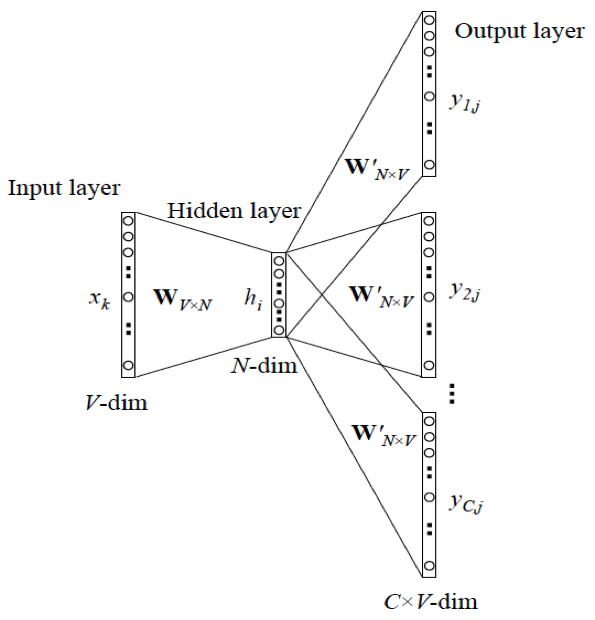
出力ベクトルはC個(本記事はn-1個、ここではC=n-1)、\(W_{V*N}\)と\(W’_{N*V}\)はlookup tableと重み行列です。下の表でCBOWとSkip-Gramの共通するところ、異なるところをまとめます。
| CBOX | Skip-Gram | ||
|---|---|---|---|
| 共通 | 構造 | 入力層 + lookup table + 中間層 + 重み行列 + 出力層 | |
| 相違 | 処理対象 | 入力ベクトル:コンテキスト、出力ベクトル:対象単語 | 入力ベクトル:対象単語、出力ベクトル:コンテキスト |
| 計算複雑度 | \((n-1)(VN)^{2}\) | \((VN)^{2}\) | |
| モデル | n-1 → 1 | 1 → n-1 | |
記事のまとめ
本記事は最初にOne-hotを紹介し、One-hotの弱みを解決するため、分散表示を紹介しました。しかし、分散表示には、次元の選定と重み数値の計算は不明でした。次に、word2vecのハラワタCBOWとSkip-Gramを紹介しました。分散表示の疑問はCBOWとSkip-Gramの流れ理解に影響するため、二つのハラワタはよく理解できませんでした。
感想と残念
本記事の締め切りは6月30日でした。記事を出す前に、lookup tableと重み行列の計算方法はDavid Meyerさんの「How exactly does word2vec work?」に発見しましたが、残念ながら記事に含めることができませんでした。
次の記事
一部の読者(特にword2vecのソースコードを見た読者)は、
- word2vecをOne-hotを全然使わない
- Googleのモデルと本記事の話が全然違う
- hierarchical softmaxはどこ?
- CBOWとSkip-Gramは誕生前に、自然言語処理はどのモデル使うのか?
などの疑問があると思います。次の記事では、以下に挙げるような内容の記事を書きたいと思います。
- CBOW、Skip-Gramの祖先の紹介(基礎部分)
- なぜword2vecのソースコードと私紹介した内容が違うのか
- hierarchical softmaxとは何か
- Lookup tableと重み行列の計算式と例

