Presto で幾何データを操作してみよう
目次
はじめに
こんにちは. DATUM STUDIO の矢野です. 休日は飛行機やその航路を眺めたり, 位置情報ゲーム片手に散歩を楽しんでおります. 本日は, そんな趣味とも関連がありそうな幾何データを SQL で扱うお話をいたします.
2017年10月, Presto に geospatial 関数の機能が バージョン 0.186 で追加されました. geospatial 関数とは, 点や折れ線, 多角形といった geometry というオブジェクトを取り扱う関数で, どこに何があるのような モノの位置関係を表現し, 位置情報の処理を書きやすくします.
geospatial 関数は MySQL, PostgreSQL, SQL Server などの RDBMS では既にサポートされていますが, Presto に機能が追加・拡充されることで, 既に Presto にある大量データの活用方法が増えたり, アプローチの仕方が増えるものと思われます.
そこで, 数回にわけて geospatial 関数は初めての方にむけて基本的な関数の紹介, 活用例について書いてみたいと思います. これを書いている時点では制約はあるようですが (空間参照系を指定して処理できないなど), 現時点でも出来ることを試しながら geospatial 関数に馴染んでみてはいかがでしょうか.
Treasure Data で geospatial 関数に対応した Presto を使用できるようになっているので, Treasure Data で geospatial 関数の基本的な内容を操作しながらその使い方に慣れていきましょう!
geometry オブジェクトの生成
いきなりですが geometry オブジェクトとは何でしょうか? 辞書を引くと geometry とは幾何という意味だそうです. 上にも モノの位置関係 と書きましたが, 大まかにいうとモノがどういう位置にあるか, どういう形をしているかを座標平面上に表現するものです.
…具体例を見ていきましょう. これを書いている時点で, Presto で扱える geometry オブジェクトには次のようなものがあります.
- POINT: 1点で表される地点. 例: 人が立っている場所
- LINESTRING: 点と点を結んだ折れ線. 例: ある人が歩いたコース
- POLYGON: 中身のある多角形. 例: 建物の敷地
- (さらに, 複数の POINT を束ねた MULTIPOINT, 複数の LINESTRING を束ねた MULTILINESTRING, 複数の POLYGON を束ねた MULTIPOLYGON, POINT, LINESTRING, POLYGON を束ねた GEOMETRYCOLLECTION があります)
さっそく, 具体的に geometry オブジェクトを生成してみましょう.
POINT
ST_Point 関数で (x, y) 座標を指定すると, 座標平面上の点である POINT geometry が作れます.
SELECT ST_Point(1, 2); -- 点 (1, 2) を生成する
ST_Point 関数にx座標を第1引数, y座標を第2引数に指定します.

POINT(1 2) のイメージ. クエリ結果には表示されない.
Treasure Data で実行してみると, 0 とだけ表示されてしまいます. どのような POINT オブジェクトが生成されているかどうか見るには, 次のように書きます.
SELECT ST_AsText(ST_Point(1, 2));

ST_AsText 関数を適用すると, POINT で座標は (1, 2) のような文字列が得られました. 今はとりあえず深入りせず, この結果が得られたらうまく 点 (1, 2) ができた! として先に進みましょう.
LINESTRING
座標平面上の線である LINESTRING オブジェクトは, ST_LineFromText 関数を使用して生成できます.
SELECT ST_LineFromText('LINESTRING(0 0, 1 1)'); -- (0, 0) と (1, 1) を結ぶ線分ここで, ST_LineFromText の引数に見慣れない文字列が出てきました. これは WKT, well-known text と呼ばれる記法に従った文字列で, 文字列で LINESTRING を表現しています.
上の例の WKT 'LINESTRING(0 0, 1 1)' は, 点 (0, 0) から点 (1, 1) に向かう線分です. 入力の際は, x 座標と y 座標の間は半角スペースで区切ること, カンマは点と点を区切るのに使用されることに要注意です.
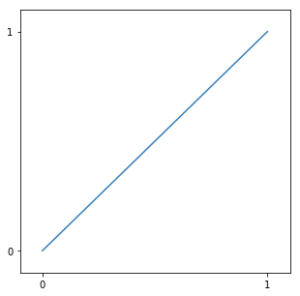
LINESTRING(0 0, 1 1) のイメージ. クエリ結果には表示されない.POINT の時の例と同じように ST_AsText 関数を適用しましょう.
SELECT ST_AsText(ST_LineFromText('LINESTRING(0 0, 1 1)'));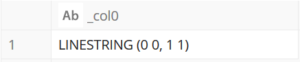
ST_LineFromText に渡した WKT 文字列がそのままクエリ結果として得られました. ST_LineFromText は, geometry 型を WKT 文字列に変換する関数なので, 全体としては ST_LineFromText が WKT → geometry の変換した後に, ST_AsText が geometry → WKT の逆方向の変換をしたため, 元の WKT に戻ってきたわけです.
これは変換して逆変換という当たり前の処理でしたが, WKT → geometry の変換が失敗する場合もありますので見てみましょう.
SELECT ST_AsText(ST_LineFromText('LINESTRING(0 0 1 1)')); -- WKT に誤りがある (カンマがない)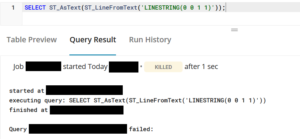
上の例では2点を真っ直ぐ結ぶ線分でしたが, 折れ線も表現できます. 折れ線を表現するには, 点をつなげて表現します.
SELECT ST_AsText(ST_LineFromText('LINESTRING(0 0, 1 1, 1 0, 2 0)'));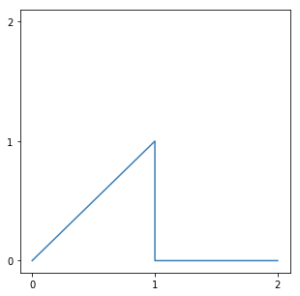
LINESTRING(0 0, 1 1, 1 0, 2 0) のイメージ. クエリ結果には表示されない.長くなりましたので LINESTRING の生成についてまとめましょう. ST_LineFromText に LINESTRING の WKT を指定すると LINESTRING geometry が得られます.
POLYGON
多角形 POLYGON は, ST_Polygon に POLYGON の WKT を指定すると POLYGON geometry が得られます.
SELECT ST_AsText(ST_Polygon('POLYGON((0 0, 0 10, 10 10, 10 0, 0 0))'));
POLYGON((0 0, 0 10, 10 10, 10 0, 0 0)) のイメージ. クエリ結果には表示されない.POLYGON の WKT は, 多角形の頂点を順に結んで囲われる領域です. LINESTRING との比較で, LINESTRING と POLYGON でそれぞれ正方形を書いてみました. LINESTRING は外周のみ, POLYGON は中身も詰まっている図形が得られます.
SELECT ST_LineFromText('LINESTRING(0 0, 0 1, 1 1, 1 0, 0 0)');
SELECT ST_Polygon('POLYGON((0 0, 0 1, 1 1, 1 0, 0 0))');
ここで, POLYGON の WKT にある括弧の組の数に注意です. LINESTRING のときは1組の括弧の開閉でしたが, 上の例では2組開閉しています. その理由は, POLYGON は穴の開いた多角形も表現できるからです. WKT の内側の各個の組に2つ目以降は穴の領域を指定できます.
SELECT ST_AsText(ST_Polygon('POLYGON((0 0, 0 10, 10 10, 10 0, 0 0), (2 2, 2 3, 3 3, 3 2, 2 2), (7 7, 9 7, 9 9, 7 9, 7 7))'));
上は, 2つの正方形の穴が開いた例です.
geometry オブジェクトを操作しよう
geometry オブジェクトを生成できたものの, どのようなメリットがあるのか geometry オブジェクトらしい処理をいくつか書いてみましょう.
ここで紹介するもの以外にも多数 geospatial 関数があるので, リファレンスに目を通して, いろいろ試してみることをおすすめします.
点が動いた距離
ある敷地内で防犯用カメラで来場する人を撮影・識別して, 1秒おきにその人の位置を取得できたとしましょう. 得られたデータは次のような motion テーブルだったとします.
| person_id | sequence | x | y |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 1 | 2 | 1 | 0 |
| 1 | 3 | 0 | 1 |
| 1 | 4 | 2 | 1 |
| 1 | 5 | 2 | 2 |
CREATE TABLE motion ( person_id INT, sequence INT, x DOUBLE, y DOUBLE ); INSERT INTO motion (person_id, sequence, x, y) VALUES (1,1,0,0), (1,2,1,0), (1,3,0,1), (1,4,2,1), (1,5,2,2);
person_id は個々の来場者を識別する番号, sequence をデータの連番, x, y を x, y 座標とします. このとき, 個々の来場者ごとに合計でどれぐらいの距離を移動したかを計算してみましょう.
SELECT
m1.person_id
, SUM(ST_Length(ST_LineFromText('LINESTRING('
|| CAST(m1.x AS VARCHAR) || ' ' || CAST(m1.y AS VARCHAR) || ','
|| CAST(m2.x AS VARCHAR) || ' ' || CAST(m2.y AS VARCHAR) || ')'
))) person_len
FROM
motion m1
INNER JOIN motion m2
ON m1.person_id = m2.person_id
AND m1.sequence + 1 = m2.sequence
GROUP BY m1.person_id;
このクエリの処理方針は, sequence が隣り合う点に線分を引き, その線の長さを合計して求めるクエリです. 隣り合う x と y の値から LINESTRING を生成するところで WKT 文字列を構築するための連結処理が煩雑に見えますね.
結果は \(5.414213562373095…\) です. 他方, 隣り合う点を LINESTRING として扱い, その距離を ST_Length で計算した結果は:
- \((0, 0)\) と \((1, 0)\) の距離: \(\sqrt{(0-1)^2 + (0-0)^2} = \sqrt{1} = 1\)
- \((1, 0)\) と \((0, 1)\) の距離: \(\sqrt{(1-0)^2 + (0-1)^2} = \sqrt{2} = \sqrt{2}\)
- \((0, 1)\) と \((2, 1)\) の距離: \(\sqrt{(0-2)^2 + (1-1)^2} = \sqrt{4} = 2\)
- \((2, 1)\) と \((2, 2)\) の距離: \(\sqrt{(2-2)^2 + (1-2)^2} = \sqrt{1} = 1\)
合計して, \(1 + \sqrt{2} + 2 + 1 = 4 + \sqrt{2} = 5.414213562373095\dots\)
LINESTRING に変換して ST_Length を適用するほか, 1行ごとに POINT geometry に変換し, 隣り合う sequence で POINT 同士を ST_Distance で計算する方法もあります. こちらの場合, 文字列連結の必要がなく, クエリも短くて済みます.
WITH motion_point AS (
SELECT person_id, sequence, ST_Point(x, y) point
FROM motion
)
SELECT
m1.person_id
, SUM(ST_Distance(m1.point, m2.point)) person_len
FROM
motion_point m1
inner join motion_point m2
ON m1.person_id = m2.person_id and m1.sequence + 1 = m2.sequence
GROUP BY m1.person_id;お部屋の広さ
エレベータを中央に配した住居の間取りが少し前に話題になりました. あの間取り図のようなお部屋を題材に, 部屋面積を測ってみましょう.
今回考える間取りは, 中心に一辺 4m の正方形状のエレベータホール, その周りに 4m 幅の洋室, その周りに 2m 幅のバストイレ, さらにその周りに 4m 幅の LDK があるとします.
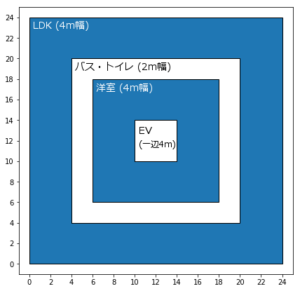
MULTIPOLYGON で外側の LDK 部分と 内側の洋室部分を分けて表現します. そしてその面積を求めるには, ST_Area を用います.
SELECT
ST_Area(
ST_GeometryFromText(
'MULTIPOLYGON(
((0 0, 24 0, 24 24, 0 24, 0 0), (4 4, 20 4, 20 20, 4 20, 4 4)),
((6 6, 18 6, 18 18, 6 18, 6 6), (10 10, 14 10, 14 14, 10 14, 10 10))
)'
)
);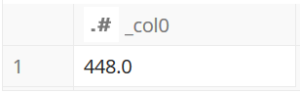
学校の算数の試験では, どういう形状かひとつひとつ確認しながら足し算引き算を工夫して計算すると思いますが, geometry オブジェクトで表現できれば ST_Area で統一的に面積を求められ, クエリもわかりやすくてよいですね.
まとめ
以上, Presto に追加された geospatial 関数の紹介として geometry オブジェクトを生成し, 簡単な計算を試してみました. 次回からは, geospatial 関数を用いてより実際にありそうな設定の問題に取り組んでみたいと思います.
繰り返しになりますが, ぜひリファレンスを読んで, いろいろ試してみてください.
DATUM STUDIOでは様々なAI/機械学習のプロジェクトを行っております。
詳細につきましてはこちら
詳細/サービスについてのお問い合わせはこちら

