ノンパラメトリックベイズ法とその応用(1)―Dirichlet過程
数回に分けて,ノンパラメトリックベイズ法の基本と応用を紹介します.今回は,ノンパラメトリックベイズ法の簡単な紹介と,理論の中核となるDirichlet過程を紹介します.
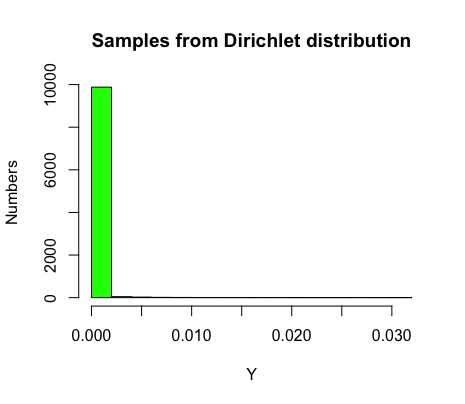 上の図は,\(k = 10000\) , \(\alpha = 0.001\) としてDirichlet分布に従うサンプルから作成したヒストグラムです.横軸が \(Y_i\) の値,縦軸が \(Y_i\) の個数に対応しています.ちょっとわかりにくいので,縦軸の範囲を限定してみます:
上の図は,\(k = 10000\) , \(\alpha = 0.001\) としてDirichlet分布に従うサンプルから作成したヒストグラムです.横軸が \(Y_i\) の値,縦軸が \(Y_i\) の個数に対応しています.ちょっとわかりにくいので,縦軸の範囲を限定してみます:
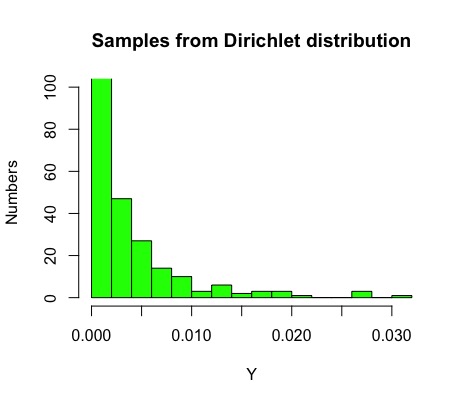 \(Y_i\) がほとんど \(0\) に近い値を取っている様子が伝わるかと思います. つまり,\(k\)-平均法によるクラスタリングで言えば,\(k\) がクラスタ数と対応するような手法を考えれば,大きな \(Y_i\) に対応するクラスタのみを用いることで,(最初は大きな次元を考えていたとしても)自動的に次元を落とすことができるというイメージを持ってください.
\(Y_i\) がほとんど \(0\) に近い値を取っている様子が伝わるかと思います. つまり,\(k\)-平均法によるクラスタリングで言えば,\(k\) がクラスタ数と対応するような手法を考えれば,大きな \(Y_i\) に対応するクラスタのみを用いることで,(最初は大きな次元を考えていたとしても)自動的に次元を落とすことができるというイメージを持ってください.
ノンパラメトリックベイズ法とは
ノンパラメトリックベイズ法は,Ferguson (1973)によって導入された手法です.最近では Ghosalとvan der Vaartによる書籍も出版されたようです. ここでのノンパラメトリックとは,一般的なノンパラメトリック法として起想されるWilcoxonの順位和検検定などとは異なり,無限次元のパラメータ考えるという意味です.もう少し詳しく言うならば,無限次元のモデルを前提に解析を行い,実際に効いている有限次元の情報を取り出す,というものです.例えば,\(k\) -平均法によるクラスタリングでは,通常はクラスタ数 \(k\) を情報量基準などに基づいて決定する必要がありますが,ノンパラメトリックベイズ法を用いる場合には分析の結果 \(k\) の事後分布が得られるといった流れで分析を行います.したがって,\(k\) を事前に決定する必要がなくなります.一見,極めて汎用性が高いようにも見えますが,相当な計算機的なパワーを要求され,高次元のデータに適用しようとすると次元の呪いを強く受けるなど,欠点も存在します.Dirichlet過程について
ノンパラメトリックベイズ法を用いる上で重要なDirichlet分布及びDirichlet過程について解説します.Dirichlet分布
\(\mathrm{Ga} (\alpha,\beta)\) を,形状パラメータ \(\alpha\),尺度パラメータ \(\beta\) を持つガンマ分布とします.つまり,\(\mathrm{Ga} (\alpha,\beta)\) の確率密度関数は \(z \geq 0\) に対して \[ f(z|\alpha,\beta) = \frac{e^{-z/\beta} z^{\alpha-1}}{\Gamma(\alpha) \beta^{\alpha}} \] となります.ここで,\(\Gamma (\alpha)\) はガンマ関数 \[ \Gamma (\alpha) = \int^{\infty}_{0}x^{\alpha -1 }e^{-x} dx \] です.次にこのDirichlet分布を多次元化します:定義 \({\alpha_1,\alpha_2,\ldots,\alpha_k} \geq 0\) のうち少なくとも一つは正とし, \(i=1,2,\ldots,k\) に対して \(Z_i\) を \(\mathrm{Ga} (\alpha_i,1)\) に従う独立な確率変数とする.ここで,\(i=1,2,\ldots,k\) に対して \[ Y_i = \frac{Z_i}{\sum^{k}_{i=1} Z_i} \] とする.いま,\((Y_1,Y_2,\ldots,Y_k)\) の同時分布を,パラメータ \((\alpha_1, \alpha_2, \ldots, \alpha_k)\) を持つDirichlet分布(\(\mathrm{Dir} (\alpha_1,\alpha_2,\ldots,\alpha_k)\))とよぶ.ここで,\(\alpha > 0\) に対し, \(\alpha_i = \alpha / k,\,i = 1,2, \ldots, k\) としてみます.すると,大きな \(k\) に対しては \(Y_i\) が偏った値を取りやすくなります.
 上の図は,\(k = 10000\) , \(\alpha = 0.001\) としてDirichlet分布に従うサンプルから作成したヒストグラムです.横軸が \(Y_i\) の値,縦軸が \(Y_i\) の個数に対応しています.ちょっとわかりにくいので,縦軸の範囲を限定してみます:
上の図は,\(k = 10000\) , \(\alpha = 0.001\) としてDirichlet分布に従うサンプルから作成したヒストグラムです.横軸が \(Y_i\) の値,縦軸が \(Y_i\) の個数に対応しています.ちょっとわかりにくいので,縦軸の範囲を限定してみます:
 \(Y_i\) がほとんど \(0\) に近い値を取っている様子が伝わるかと思います. つまり,\(k\)-平均法によるクラスタリングで言えば,\(k\) がクラスタ数と対応するような手法を考えれば,大きな \(Y_i\) に対応するクラスタのみを用いることで,(最初は大きな次元を考えていたとしても)自動的に次元を落とすことができるというイメージを持ってください.
\(Y_i\) がほとんど \(0\) に近い値を取っている様子が伝わるかと思います. つまり,\(k\)-平均法によるクラスタリングで言えば,\(k\) がクラスタ数と対応するような手法を考えれば,大きな \(Y_i\) に対応するクラスタのみを用いることで,(最初は大きな次元を考えていたとしても)自動的に次元を落とすことができるというイメージを持ってください.
Dirichlet過程
上で定義したDirichlet分布を用いて,Dirichlet過程を定義します.定義 \(\chi\) を完備かつ可分な距離空間とし,\(\mathcal{A}\) を \(\chi\) のボレル \(\sigma\) -加法族 とする.\(\alpha\) を \(0 < \alpha (\chi) < \infty\) を満たす \((\chi , \mathcal{A})\) の測度とする.この時,ランダム測度 \(\mathrm{D}\) が \(\chi\) の全ての可測分割 \({B_1,B_2,\ldots,B_k}\) に対して \((D(B_1),D(B_2),\ldots,D(B_k))\) が \(\mathrm{Dir} (\alpha (B_1), \alpha (B_2), \ldots, \alpha (B_k))\) に従う時,\(\mathrm{D}\) をパラメータ \(\alpha\) のDirichlet過程という.Ferguson(1973)の定義1. を参考にしつつ書いているので数学的な用語が出てきます.直感的には,雑草が一面に茂っている庭を重複なく分割(分割の方法は \(\alpha\) による)した場合,それぞれの分割に生えている雑草の長さの和が,それぞれDirichlet分布に従っている」ような状況を想像してください. (注:本当に雑草の生え方がDirichlet過程に従っている訳ではありません! 従っている可能性はあるかもしれませんが…) Dirichlet過程では,分割の”方法”に柔軟性を持たせているイメージを持っていただければと思います. 以上の議論でDirichlet過程の定義や性質を述べましたが,このようなDirichlet過程が本当に構成できるのかどうかはまた別の問題です,もちろん,構成できるのですが,その構成方法については Sethuraman (1994) 等を参考としてください.

