調整済み散布図
初めまして。DATUM STUDIOの超絶怒涛のスーパーアイドルこと、ともにゃんです。趣味は猫の写真を眺めたり、出会い系アプリで未来の彼女を探したりすることです。はやく2番目の趣味をやめたいです☆(ゝω・)v
今回は線形回帰分析において変数を選ぶ時に役立つ、調整済み散布図と呼ばれるものをご紹介したいと思います☆(ゝω・)v
1. 線形回帰のモデリング
回帰分析という手法の名前を耳にしたことがあるかもしれません。回帰分析は、例えば「気温が高い日はアイスコーヒーの売上が伸びる」といったように、要因(気温)と結果(アイスコーヒーの売上)の関係を見つけたい時に、そしてその関係をモデル化する際の手法の1つです。線形回帰モデルはベーシックな統計の教科書に載っていますので、読者の方は線形回帰がどのようなものかイメージできると仮定して、本稿ではあまり教科書には載っていない線形回帰モデルのモデリング方法をご紹介します。
1.1. 調整済み散布図による変数選択
線形回帰モデルにおけるモデリングとは、線形回帰の課される仮定を満たしつつ「結果をよく説明する説明変数の組みをみつける」ことです。つまり、手元にある説明変数のうち、どの説明変数を使うか決めてあげることをいいます。このことを変数選択と呼んだりします。
以下のFigure1やFigure2は、散布図行列と呼ばれるプロットです。散布図行列は、データ間の1対1の関係をひと目でみることができて非常に便利です。しかし、この散布図行列だけをみて変数選択をするのは危険です。それを実感するために、以下の簡単な例を見てみましょう。
| y | x1 | x2 |
|---|---|---|
| 1 | 0 | 1 |
| -1 | 1 | -2 |
| -1 | 2 | -3 |
表1をみて分かるように、x1 + x2がyになっていることが分かります。つまり、x1の回帰係数は1ということになります。しかし、このデータの散布図行列をみてみましょう。
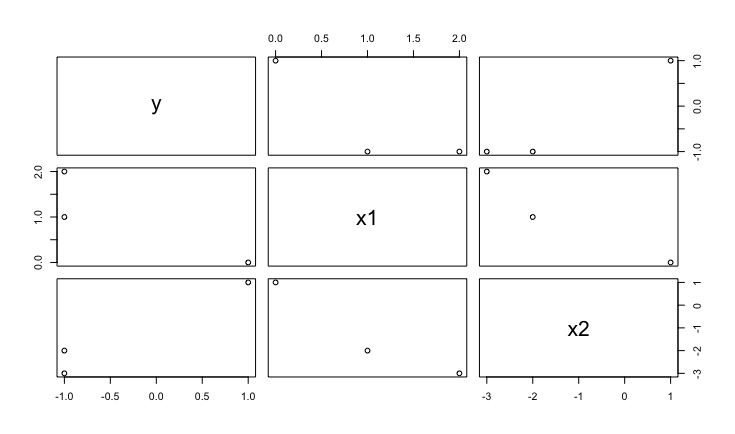
上から1行目、左から2列目の(x1, y)のプロットを見てください。この図を見る限りは、x1が大きくなればyの値は小さくなるという負の相関がありそうです。つまり、yとx1の単回帰モデルを構築した時に、その回帰係数は負になります。このことは、x1とx2を同時に考慮した時、つまり重回帰モデルを構築したときにx1の回帰係数が1という正の相関があることと矛盾しています。この理由は、x1とx2の間に負の相関があるためです。このことはx1の回帰係数は単回帰と重回帰とでは異なった意味を持っており、全く異なった値をもつことがあるということを示しています。そして、たとえある説明変数がが他の説明変数に対して強い相関を持っていないとしても、yとxのすべてを含んだ関係の中でのyの特定のxに対する真の依存関係は、yのxに対する散布図では把握するのが難しいです。散らばりが大きい場合は変数間の関係がぼやけてしまうためです。
以上の例から、単純に説明変数と目的変数の1対1の散布図を見るだけでは、重回帰モデルにおいてある変数が目的変数にどのような影響を与えるのかを見るのは難しいということがわかります。では、どのようなプロットを描けば、重回帰モデルにおいて他の変数を考慮しながらある変数の目的変数に対する影響をみることができるでしょうか。その答えの1つとして調整済み散布図というプロットがあります。
1.2. 調整済み散布図
ここでは、調整済み散布図の描き方を紹介した後に、調整済み散布図が何を表しているのかを説明します。 次のような状況を考えてみます:
目的変数をyi, i = 1, …, N、説明変数をxi = (xi1, …, xi, p)とします。まずはじめにxi1, i = 1, …, Nを使って単回帰をしたとします: \[ \begin{aligned} y_{i} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{i1} + \hat{\epsilon_{i}},\ i=1,\ldots,N \label{eq:reg1}\end{aligned} \] ここで\(\hat{\beta_{0}}\)は切片項、\(\hat{\beta_{1}}\)は1番目の変数についての回帰係数、\(\hat{\epsilon_{i}}\)は残差です。そしてこのモデルに2番目の変数xi2, i = 1…,Nを入れる意味があるかどうかを調べたいとします。このときに調整済み散布図を書きます。
上記式中の\(\hat{\epsilon_{i}}\)をyi2*と読み替えます。このとき、調整済み散布図の描き方は次の通りです:
Step 1: xi2を目的変数、xi1を説明変数として単回帰をする: \[ \begin{aligned} x_{i2} = \hat{\gamma_{0}} + \hat{\gamma_{i}}x_{i1} + x_{i2}^{\ast} \label{eq:reg2}\end{aligned} \]
Step 2: \( (x_{i2}^{\ast}, \hat{\epsilon_{i}}) = (x_{i2}^{\ast}, y_{i2}^{\ast}) \)をペアにして散布図を描く
これだけです。上記の例における、この調整済み散布図の直感的な意味を説明しましょう。
まず式([eq:reg1])において、残差\( \hat{\epsilon_{i}} = y_{i2}^{\ast} \)は”説明変数xi1では説明できなかった要素“です。もしxi1でyiを完全に説明できるのであれば残差は0となるはずですから、残差が値を持つということはxi1では説明できていない部分があるということになります。また、式([eq:reg2])についても同じことが言えて、残差xi2*は”説明変数xi1では説明できなかったxi2の要素”、つまり、“新たにモデルに組み込みたいと思っている変数xi2から、既にモデルに組み込まれている変数xi1の影響を取り除いて残った部分”と解釈できます。したがってStep 2では、
“yiの要素の中で、既にモデルに組み込まれている説明変数xi1で説明できなかった部分”と、“新たにモデルに組み込みたいと考えている説明変数xi2から、既にモデルに組み込まれている説明変数xi1の影響を取り除いたもの”
を散布図として描いていることになります。もし、調整済み散布図から(xi2*, yi2*)の間に相関が見られたならば、既にモデルに組み込まれている変数xi1の影響を取り除いてもなお、追加しようとしている変数xi2にはyiを説明する力があるということになり、説明変数xi2をモデルに追加することをにする、といった判断が可能になります。
以上の話では、yi、xi1、xi2を使って調整済み散布図について説明をしましたが、一般的な場合についてまとめておきます。
Step 0:p − 1個の説明変数を使った回帰モデルを構築します: \[ \begin{aligned} y_{i} = \beta_{0} + \sum_{j=1}^{p-1}\beta_{j}x_{ij} + y_{ip}^{\ast},\ i = 1,\ldots,N \label{eq:reg3}\end{aligned} \] ここでyip*は残差とします。
Step 1: 新たに説明変数xipをStep 0の回帰モデルに入れることを考えます。新たに追加したいと考えている変数xipから、既にモデルに組み込まれているp − 1個の変数xi1, …, xip − 1の影響を取り除くために、xipとp − 1個の変数xi1, …, xip − 1の回帰を行います: \[ \begin{aligned} x_{ip} = \hat{\gamma_{0}} + \sum_{j=1}^{p-1}\gamma_{j}x_{ij} + x_{ip}^{\ast},\ i = 1,\ldots,N \label{eq:reg4}\end{aligned} \] ここでxip*は残差とします。
Step 2:(xip*, yip*)をペアにして散布図を描く。
さて、上記では調整済み散布図の直感的な説明をしました。実はこの直感は、数学的にも正しいことが分かっています。つまり、以下のことが言えます:
p個の説明変数xi1, …, xipで目的変数yiを回帰した時の回帰モデルを \[ \begin{aligned} y_{i} = \hat{\alpha_{0}} + \sum_{j=1}^{p}\hat{\alpha_{j}}x_{ij} + \hat{\epsilon_{i}},\ i=1,\ldots,N\end{aligned} \] とします。また、Step 0の式とStep 1の式におけるyip*とxip*について、切片項なしの単回帰モデルを \[ \begin{aligned} y_{ip}^{\ast} = \hat{\eta_{p}}x_{ip}^{\ast} + \hat{\epsilon_{i}}^{\ast},\ i=1,\ldots,N\end{aligned} \] とします。このときに \[ \begin{aligned} \hat{\alpha_{p}} &=& \hat{\eta_{p}}\\ \hat{\epsilon_{i}} &=& \hat{\epsilon_{i}}^{\ast}\end{aligned} \] が言えます。いきなりp個の変数で回帰をした時のxipの係数と、他のp − 1この変数の影響を除いた後に回帰をした時のxip*が同じになり、それぞれのケースにおける残差も同じになるということです。つまり、調整済み散布図をみれば、その視覚的な傾向と重回帰をしたときの実際の係数の値に矛盾がおきなくなります。1.3節では単純な散布図による視覚的な傾向と、重回帰のときの係数との間で矛盾が起きていることをみましたが、調整済み散布図を用いればそういったことが起きなくなります。
上記事実の証明は、難しくはありませんが長くなるので今回は割愛します。
1.3. 調整済み散布図の例
それでは、実際に調整済み散布図をRを使って描いてみます。ここでは、オリジナルのデータを発生させてそれを使用します。以下のコードを実行してみます:
# 乱数シードの指定
set.seed(1234)
# データ数の指定
n = 200
# 説明変数を発生
x1 <- rnorm(n, 5, 1)
x2 <- -x1 + rnorm(n, 0, 0.7)
x3 <- rnorm(n, 0, 1)
# 真の回帰係数の指定
b0 <- 1
b1 <- 3
b2 <- 2
b3 <- 0.01
# 説明変数と真の回帰係数を使用して目的変数を発生
y <- b0 + b1*x1 + b2*x2 + b3*x3 + rnorm(n, 0, 1)
# y, x1, x2, x3をデータフレームとしてまとめる
d <- as.data.frame(cbind(y, x1, x2, x3))
# 散布図行列
pairs(d)すると図2のような散布図行列が描かれます。
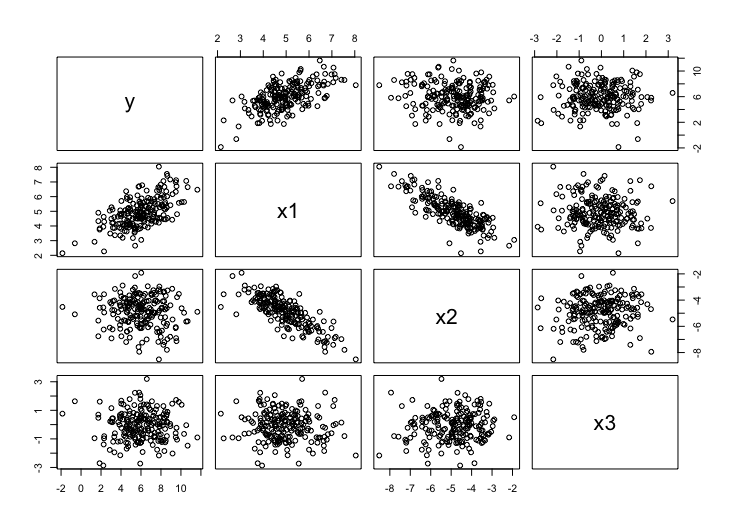
一見、目的変数yと説明変数x2の間には相関があまりないようにデータを生成しました。実際に相関係数を計算すると-0.0993818となります。説明変数と説明変数の1対1の散布図だけを眺めていては、もしかするとx2をモデルから排除してしまうかもしれません。しかし、調整済み散布図を描けばx2を解析から除外してしまうことを回避できます。
x1を説明変数として使用すると決めたとします。このモデルにx2を組み込むべきかどうかを散布図行列を描いて確認してみましょう。まず、既にモデルに組み込まれているx1では説明できないyの部分を求めるために、yをx1で回帰し、そのときの残差 y2_ast を以下のように計算します:
y2_ast <- lm(y x1, d)$residuals続いて、新たにモデルに組み込みたいと考えているx2から、既にモデルに組み込まれているx1の影響を排除するために、x2をx1で回帰し、その時の残差 x2_ast を以下のように計算します:
x2_ast <- lm(x2 x1, d)$residualsそして最後に、以下のようにして上記で求めた x2_ast と y2_ast の散布図を描けば、調整済み散布図の完成です(図3):
plot(x2_ast, y2_ast)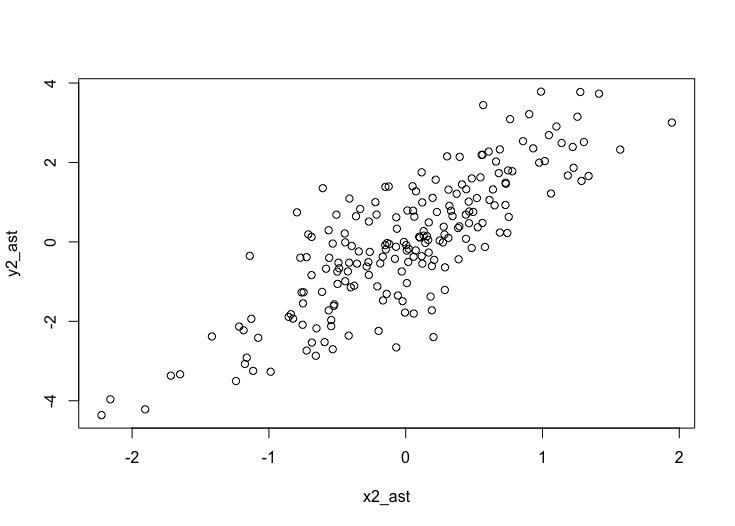
ちゃんと真の係数 b2 = 2 の情報がこの調整済み散布図から見て取れると思います。
同様にして、x3をモデルに組み込むべきかどうかを確認するために以下のコードを実行します:
y3_ast <- lm(y x1+x2, d)$residuals
x3_ast <- lm(x3 x1+x2, d)$residuals
plot(x3_ast, y3_ast)yとx3の調整済み散布図(図4)を眺めると、x3にはyを説明する力はないようです。
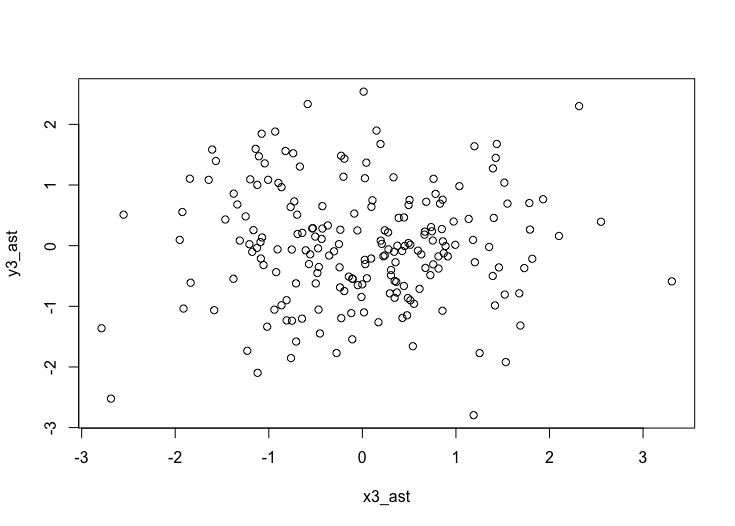
よって、最終的にx1とx2を説明変数としたモデルを構築します(図5)。
fit <- lm(y x1+x2, d)
summary(fit)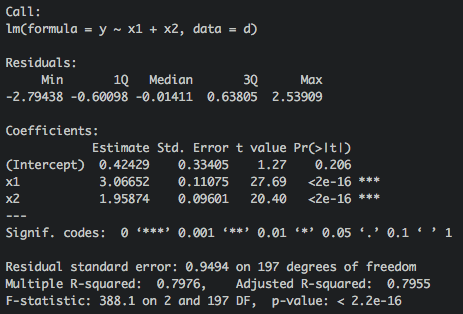
おわりに
線形回帰モデルはベーシックな教科書には必ず載っているモデルですし、RやPythonを使って気軽にモデルを構築することができるため、非常に身近なモデルです。しかし、線形回帰モデルは意外と奥深いモデルなのです。調整済み散布図を描くことである変数から他の変数の影響を取り除くと目的変数に対してどのような影響が残るのかといったデータ理解も進むと思います。調整済み散布図を描きながら、是非重回帰モデルを構築してみてください。
次回は今回紹介した線形回帰モデルを、ベイズ統計学の枠組みへ拡張する方法を紹介します。
それでは、ともにゃんでした☆(ゝω・)v

