状態空間モデル
時系列の売り上げデータなどに、広告費などの説明変数だけではどうしても説明できない、長期的な変動が存在することがあります。このようなデータを、説明変数で説明できる変動と、説明できない長期的な変動に分解したい時、どうすればよいでしょうか。
そのような時、状態空間モデルの考え方を使って、長期的な変動をトレンド成分として推定することができます。トレンド成分とは、前の時点の値から正規分布に従って変動する成分のことです。正規分布のばらつきが小さければ、滑らかに変動していくことになります。
実際にStanを使ってこのようなモデルを推定してみましょう。まず、Rで模擬データを生成します。
generate_data.R
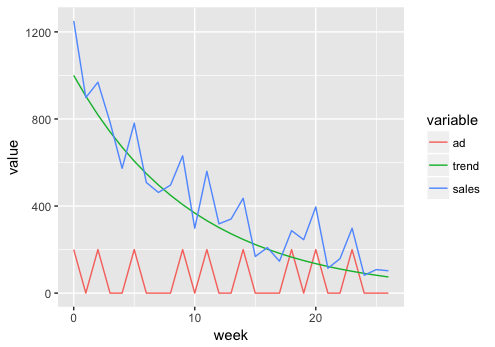
ここでは、広告費の投入 ad と商品の売り上げ sales の関係を考えます。売り上げのトレンド成分 trend は、商品発売直後は多いですが、指数関数に従って減少するとします。トレンド成分と広告費投入の和に正規分布に従うノイズを加えたものが、sales になると考えます。
このデータからトレンド成分 trend と広告費投入の効果 coef_ad を推定するStanのコードは、次のようになります。
trend.stan
Stanでは、data ブロックで読み込むデータを、parameters ブロックで各時点のトレンド成分を含むパラメータを、model ブロックでモデル本体を、generated quantities ブロックで、推定結果から生成される値を、それぞれ定義します。
data ブロックでは、sales の確率分布にポアソン分布を採用しているため、変数 sales に 整数型を指定していることに注意してください。
parameters ブロックでは、パラメータの変数の定義とともに、探索範囲も定義しています。 coef_ad は広告費の効果を表す係数、trend_ini はトレンド成分の初期値、theta はトレンド成分の変動の大きさです。各時点のトレンド成分 trend もパラメータとして推定します。
model ブロックでは、トレンド成分が前の時点の値から、標準偏差 theta の 正規分布に従って変動することを定義しています。トレンド成分と、広告費に係数をかけたものの和が sales の推定値 sales\_hat です。 target はモデルのデータへの当てはまりを示す対数尤度の和を格納する、特別な変数です。これにポアソン分布に従う対数尤度を足しています。
generated quantities ブロックでは、sales の各時点の推定値 sales_hat_out を出力させています。
それでは、Rのパッケージ rstan を使ってこのStanコードからモデルを推定し、プロットしてみましょう。
estimate_model.R
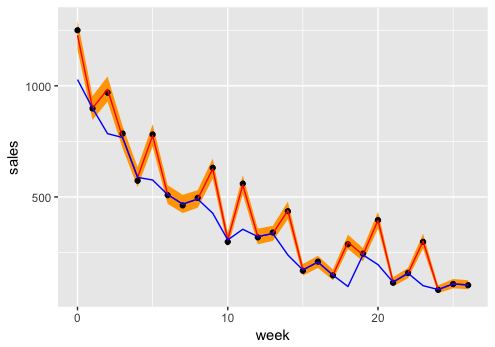
黒丸が実測値、赤線が推定値、オレンジの背景が推定値の95%信用区間、青線がトレンド成分です。 sales の時系列にモデルがよくあてはまっていることがわかると思います。赤線の推定値と青線のトレンド成分の差が、広告費で説明できた成分になります。
次に、広告費の効果を示す係数 coef_ad は1と推定されているでしょうか。
plot_density.R
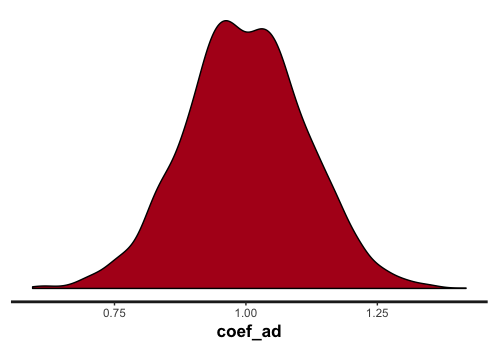
正解は1ですが、ほとんどバイアスなく推定されているようです。
このように、状態空間モデルの考え方を使うことで、時系列のデータを、説明変数で説明できる成分と、説明できないが滑らかに変動する、トレンド成分に分解することができます。
このようなデータに出会った時は、状態空間モデルを使ってみてはいかがでしょうか。
library(ggplot2)
library(reshape2)
week <- seq(from = 0, to = 26)
trend <- 1000 * exp(-0.1 * time)
ad <- rep(c(200, 0, 200, 0, 0, 200, 0, 0, 0), times = 3)
sales <- trend + ad + rnorm(length(trend), mean = 0, sd = 50)
generated.data <- data.frame(week = week, ad = ad, trend = trend, sales = sales)
df.plot <- melt(generated.data, id.vars = "week")
ggplot(df.plot) +
geom_line(aes(x = week, y = value, group = variable, color = variable))
data {
int N_week;
vector[N_week] ad;
int sales[N_week];
}
parameters {
real coef_ad;
real trend_ini;
real theta;
vector[N_week] trend;
}
model {
real sales_hat;
for (i in 1:N_week) {
if (i == 1) {
trend[1] ~ normal(trend_ini, theta);
} else {
trend[i] ~ normal(trend[i-1], theta);
}
sales_hat = trend[i] + coef_ad*ad[i];
target += poisson_lpmf(sales[i] | sales_hat);
}
}
generated quantities {
vector[N_week] sales_hat_out;
for (i in 1:N_week) {
sales_hat_out[i] = trend[i] + coef_ad*ad[i];
}
} library(rstan)
data <- list(
N_week = length(week),
ad = ad,
sales = round(sales)
)
model <- stan_model("trend.stan")
fit <- sampling(model, data = data)
df.summary <- summary(fit)$summary
df.plot <- with(data, data.frame(
week = week,
observation = sales,
estimation = df.summary[grep("^sales_hat_out", rownames(df.summary)), "mean"],
lower = df.summary[grep("^sales_hat_out", rownames(df.summary)), "2.5%"],
upper = df.summary[grep("^sales_hat_out", rownames(df.summary)), "97.5%"],
trend = df.summary[grep("^trend\\[", rownames(df.summary)), "mean"]
))
library(ggplot2)
ggplot(df.plot) +
geom_ribbon(aes(x = week, ymin = lower, ymax = upper), fill = "orange") +
geom_point(aes(x = week, y = observation)) +
geom_line(aes(x = week, y = estimation), color = "red") +
geom_line(aes(x = week, y = trend), color = "blue") +
labs(y = "sales")
stan_dens(fit, pars=c("coef_ad"))

