networkxで全国名字ネットワークを可視化してみた
こんにちは。データムスタジオの林です。最近、気温が変わりやすく外出時の服装に迷うことが多いです。皆さんもお体にはお気をつけください。
さて、今回のテーマについてですが、自分の名字が「森林系」と聞いて、「田中」「吉田」「山田」等名字の関連が気になっていますので、今回は全国名字のネットワーク分析をやってみたいと思います。
では、早速始めましょう!
目次
1. データを読み込む
今回の分析用データは名字由来netの全国名字ランキングを使います。このランキングには全国1位から40000位の名字と人数を網羅しています(合計1.24億人)。
まずは必要なパッケージをインポートし、データを読み込みます。
from collections import Counter
from itertools import chain, combinations
import numpy as np
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.rcParams['font.family'] = 'IPAexGothic'
# データを読み込む
df = pd.read_csv('surnames.csv')
# 同の字点(々)を本来の漢字に入れ替える
has_iter = df.loc[df['name'].str.contains('々'), 'name'].str.extract(r'(.*)々(.*)', expand=False)
df.loc[df['name'].str.contains('々'), 'name'] = has_iter[0]*2 + has_iter[1]
print(df.head(10))処理したデータはこんな感じです:
| name | count | |
| 0 | 佐藤 | 1887000 |
| 1 | 鈴木 | 1806000 |
| 2 | 高橋 | 1421000 |
| 3 | 田中 | 1343000 |
| 4 | 伊藤 | 1081000 |
| 5 | 渡辺 | 1070000 |
| 6 | 山本 | 1057000 |
| 7 | 中村 | 1051000 |
| 8 | 小林 | 1034000 |
| 9 | 加藤 | 892000 |
2. グラフ作成
# グラフを作成
G = nx.Graph()
for i, row in df.iterrows():
nodes = set(row['name'])
freq = row['count']
for n in nodes:
if G.has_node(n):
G.node[n]['freq'] += freq
else:
G.add_node(n, freq=freq)
node_combi = combinations(nodes, 2)
for u, v in node_combi:
if G.has_edge(u, v):
G.adj[u][v]['freq'] += freq
else:
G.add_edge(u, v, freq=freq)次はnetworkxパッケージのGraph()関数でグラフを作成し、df全ての行を繰り返し処理します。一つ一つの人名漢字はグラフのノードとなり、その漢字を含む名前の人数はノードのウェイトとなります。
一方、二つ漢字が同時にある名字に含まれている場合は、その二つ漢字ノード間にエッジを追加します。ノードと同様に、エッジのウェイトは端点からなる名字の人数に設定します。
これで準備完了で、分析を始めます。
3. 人名漢字別出会う確率ランキング
# 人名漢字別の確率を算出
node_freqs = [(u, d['freq']) for u, d in G.nodes(data=True)]
node_freqs = pd.Series([t[1] for t in node_freqs], index=[t[0] for t in node_freqs], name='freq')
node_freqs /= df['count'].sum() * 0.01
# 確率の最も高い漢字を棒グラフに
plt.figure(figsize=(12, 6))
node_freqs.nlargest(30).plot(kind='bar', rot=0)
plt.xlabel('人名漢字')
plt.ylabel('確率 (%)')
plt.title('人名漢字別出会う確率ランキング')
plt.tight_layout()
plt.savefig('proba.png', dpi=300)
plt.show()本番に入る前に、各漢字の出現頻度を見てみます。頻度を合計人数で割れば、「○が付く名前の人」に出会う確率が得られます。その結果:
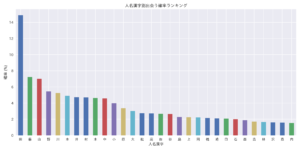
「田」が付く名前の人に出会う確率は14%強です。すなわち、7人に1人の名前が「田」を含んでいます。
4. 人名漢字の次数中心性
# 次数中心性の分布を見る
plt.hist(nx.degree_centrality(G).values(), bins=100)
plt.yscale('log')
plt.xlabel('次数中心性')
plt.ylabel('人名漢字数')
plt.title('人名漢字次数中心性の分布')
plt.tight_layout()
plt.savefig('dc.png', dpi=300)
plt.show()最も多くのノード(=漢字)と繋がっているノードが一番面白いと思いますので、次はノード別次数中心性を算出します。次数中心性とは、ノードにつながっているエッジの本数ということになります。
ちなみに、networkxのdegree_centrality()関数で計算される次数中心性が正規化されるので、定義は以下の通りです:
$latex 次数中心性 C_{D}(v) = \frac{deg(v)}{n – 1}$
ここで$latex deg(v)$はノード$latex v$と繋がっているノード数、$latex n$はグラフのノード数です。
仮にそれ自信以外の全ノードと連結しているノードがあるとすると、それが次数中心性が1になります。
算出した次数中心性をヒストグラムにすると:
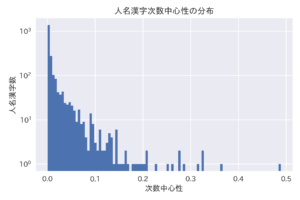
横軸は各ノードに関する次数中心性、縦軸はある次数中心性の幅に含まれるノード数ということになります。
中心性が0に近い漢字が殆どですが(左側)、一番右に割と高いノードも存在しています。(分類された漢字の少ないビンも見えるように、縦軸を対数目盛にしました。)
最大の次数中心性は0.5程度になります。
中心性のトップ3人名漢字を抽出してみると:
# 中心性のトップ3人名漢字 print(Counter(nx.degree_centrality(G)).most_common(3))
[('田', 0.48865698729582574), ('野', 0.36388384754990927), ('川', 0.3248638838475499)]
驚くことに、「田」は半数の人名漢字と、そして「野」「川」は1/3の人名漢字と組み合わせ可能です。
では、中心性の高いノードを描きましょう。
# グラフ可視化ベース関数
def draw_char_graph(G, fname, node_color='#BC002D', map_node_edge=True, **kwargs):
if map_node_edge:
kwargs['node_size'] = np.array([d['freq'] for k, d in G.nodes(data=True)]) / 1e3
kwargs['edge_color'] = [d['freq'] for u, v, d in G.edges(data=True)]
plt.figure(figsize=(12, 12))
nx.draw(G,
node_color=node_color,
edge_cmap=plt.cm.Greys,
edge_vmin=-3e4,
width=0.5,
with_labels=True,
font_family='IPAexGothic',
font_size=16,
font_color='white',
**kwargs)
plt.savefig(fname, dpi=300)
plt.show()
# 中心性の高いノードを抽出し描く
central_nodes = [k for k, v in nx.degree_centrality(G).items() if v >= 0.2]
G_central = G.subgraph(central_nodes)
draw_char_graph(G_central, 'central.png')ここは中心性が0.2を超えたノードを描きました。また、ノードの大きさはその漢字を含む人数、エッジの濃さは結ばれているノードの漢字を同時に含む人数を表しています。
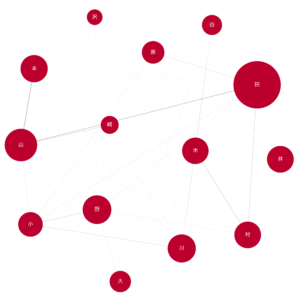
5. 中心性の最も高い人名漢字のネットワーク
続いては次数中心性トップ3の関連ネットワークを描きます:
# 人数閾値を算出
node_freqs = np.array([d['freq'] for u, d in G.nodes(data=True)])
freq_threshold = np.mean(node_freqs) + 2*np.std(node_freqs)
# 指定ノードを描く関数
def draw_nodes_of_interest(G, fname, node=None, node_pos=None):
if node is not None:
nodes = set(node)
elif node_pos is not None:
nodes = set(node_pos.keys())
else:
raise ValueError('Either node or node_pos must be passed')
neighbors = set(chain(*[G.neighbors(n) for n in nodes]))
neighbors = set([u for u, d in G.nodes(data=True) if d['freq'] >= freq_threshold and u in neighbors])
nodes_to_draw = nodes | neighbors
nodes_to_draw = [(u, d) for u, d in G.nodes(data=True) if u in nodes_to_draw]
edges_to_draw = [(u, v, d) for u, v, d in G.edges(data=True)
if (u in nodes and v in neighbors)
or (v in nodes and u in neighbors)]
G_int = nx.Graph()
G_int.add_nodes_from(nodes_to_draw)
G_int.add_edges_from(edges_to_draw)
node_color = ['dimgray' if u in nodes else '#BC002D' for u, d in nodes_to_draw]
if node is not None:
draw_char_graph(G_int, fname, node_color=node_color)
else:
pos = nx.spring_layout(G_int, k=2, pos=node_pos, fixed=nodes)
draw_char_graph(G_int, fname, pos=pos, node_color=node_color)
# ネットワークを描く
draw_nodes_of_interest(G, '田.png', ['田'])
draw_nodes_of_interest(G, '野.png', ['野'])
draw_nodes_of_interest(G, '川.png', ['川'])ノードが多すぎて見づらくならないように、人数閾値を計算しておいて、閾値を超えたノードのみ描きました。
5.1 田
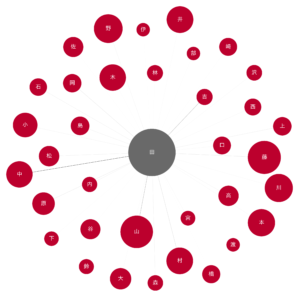
エッジの濃さから見れば、田中、吉田、山田等が一番目立つようです。
5.2 野
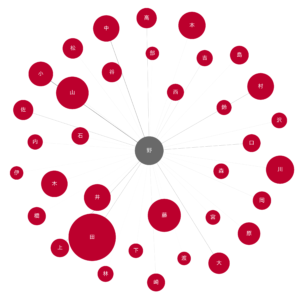
山野、中野、上野、野田、野村等が一番多いようです。
5.3 川
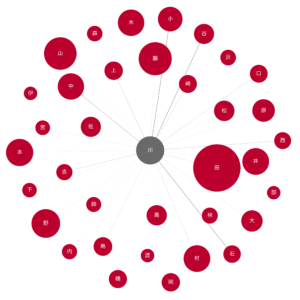
谷川、中川、石川、小川のエッジが特に目立っています。
6. 関連語のネットワーク
次は木・林・森といった関連語の隣接関係を分析します。
6.1 大・中・小
node_pos = {'大': (0.5, 1), '中': (0.5, 0.5), '小': (0.5, 0)}
draw_nodes_of_interest(G, '大中小.png', node_pos=node_pos)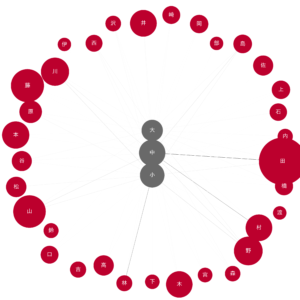
大・中・小川等が同時に存在していうように、関連語の隣接関係は似ているようです。
6.2 上・下
node_pos = {'上': (0.5, 1), '下': (0.5, 0)}
draw_nodes_of_interest(G, '上下.png', node_pos=node_pos)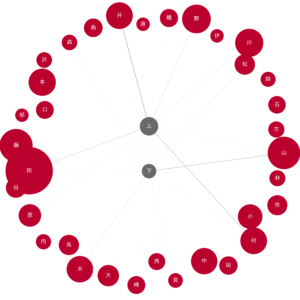
上・下は重なっている隣接もありますが、人数の多い隣接は異なります。
6.3 東・西・南・北
node_pos = {'東': (1, 0.5), '西': (0, 0.5), '南': (0.5, 0), '北': (0.5, 1)}
draw_nodes_of_interest(G, '東西南北.png', node_pos=node_pos)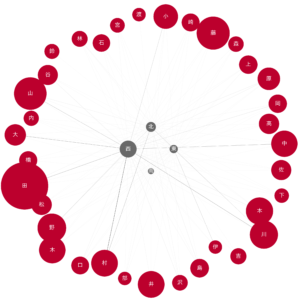
四方とも繋がっている漢字が意外と多いですが、なぜか西の隣接が一番多いです。
6.4 木・林・森(森林系)
node_pos = {'木': (0.5, 1), '林': (0.5, 0.5), '森': (0.5, 0)}
draw_nodes_of_interest(G, '木林森.png', node_pos=node_pos)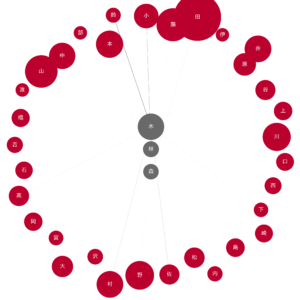
最後は森林系ですが、エッジの薄さから一部の組み合わせを除いて人数が比較的に少ないことがわかりました。
7. おまけ:最大クリーク
グラフ理論におけるクリークとは、任意の二ノード間にエッジがあるようなノード集合です。そして最大クリークとは、その中で最大のものを指しています。
よって、今回分析における最大クリークは、任意の二漢字を含む名字が存在している、最大のノード集合です。それを描くと、46個漢字から構成される巨大ネットワークとなっています。
この46個漢字より任意の二つを選んだら名字になるということです。
あなたの名字はいかがでしょうか。
# 最大クリークを見つけて描く max_cliques = sorted(nx.find_cliques(G), key=lambda x: len(x), reverse=True) draw_char_graph(G.subgraph(max_cliques[0]), 'max_clique.png', map_node_edge=False, node_size=500, edge_color='gray')
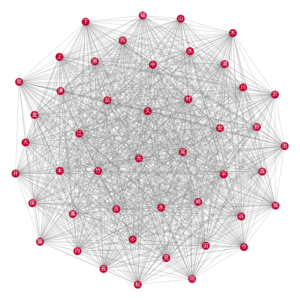
8. まとめ
最後まで読んで頂きありがとうございました。
今回はPythonのnetworkxパッケージで全国名字ネットワーク分析を行い、次数中心性の高い人名漢字を発見しました。この分析によって日本全国の名字について更に理解を深められると良いですね。
では、また次回!
参考文献
・名字由来net:https://myoji-yurai.net

