はじめに

昨今の深層学習ブームの火付け役となった事前学習を、tensorflowを使って実装してみました。 機械学習プロフェッショナルシリーズ「深層学習」、「TensorFlowで学ぶディープラーニング入門」を参考に実装を行いました。

事前学習とは

2度の冬の時代を経験した後、2006年からの深層学習ブームのきっかけとなった深層学習の精度改善手法です。 (論文PDFはこちら) 事前学習ではニューラルネットワークを学習させる際に設定する重みの初期値を、事前に別のニューラルネットワークを学習して求め、学習を最適化させます。事前学習にはRBMによるもの、自己符号化器によるものがありますが、ここでは自己符号化器を用いたものを実装します。

自己符号化器とは

自己符号化器とは、出力を入力に近づけるよう学習するニューラルネットワークです。入力に対してニューラルネットワークで変換し(Encode 符号化)、それを折り返して変換した際(Decode 復号)、元の入力に近づくように学習します。

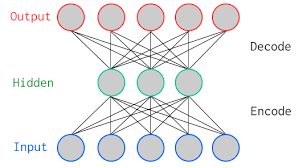
手書き文字認識データ(MNIST)を例に、自己符号化器を実装してみたものが以下になります。

# パッケージの読み込み
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
# MNISTデータの読み込み
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# 入力層のユニット数 = 784
# 中間層のユニット数 = 100 # として学習を行う num_units = 100
# 入力x
x = tf.placeholder(tf.float32, [None, 784])
# 第1層の重み、バイアス
# 分散0.01のガウス分布で初期化
w_enc = tf.Variable(tf.random_normal([784, num_units], stddev=0.01)) b_enc = tf.Variable(tf.zeros([num_units]))

# 第2層の重み、バイアス
# 分散0.01のガウス分布で初期化
w_dec = tf.Variable(tf.random_normal([num_units, 784], stddev=0.01)) b_dec = tf.Variable(tf.zeros([784]))
# 中間層の活性化関数は正規化線形関数
encoded = tf.nn.relu(tf.matmul(x, w_enc) + b_enc)
# 出力層は恒等写像
decoded = tf.matmul(encoded, w_dec) + b_dec
# 誤差関数は2乗誤差の総和
# かつ λ = 0.1の重み減衰を行う
lambda2 = 0.1
l2_norm = tf.nn.l2_loss(w_enc) + tf.nn.l2_loss(w_dec)
loss = tf.reduce_sum(tf.square(x - decoded)) + lambda2 * l2_norm
# 学習係数 0.001, のAdamのアルゴリズムをSDGに用いる
train_step = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)
# セッションを用意し、変数を初期化する
sess = tf.InteractiveSession() sess.run(tf.initialize_all_variables())
# バッチサイズ100の確率的勾配降下法を1000回行う i=0
for _ in range(1000):
    i += 1
    batch_xs, batch_ts = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs})
    if i % 100 == 0:
        loss_val = sess.run(loss,
            feed_dict={x:mnist.train.images})
        print ('Step: %d, Loss: %f'% (i, loss_val))
# 学習した重みとバイアスを抽出
w_dec_p, b_dec_p, w_enc_p, b_enc_p = sess.run([w_dec, b_dec, w_enc, b_enc])
# 訓練画像
x_train = mnist.train.images

自己符号化した画像を表示してみます。

# 自己符号化した画像の表示
n = 10 plt.figure(figsize=(20, 4))
for i in range(n): # もともとの画像
      ax = plt.subplot(2, n, i + 1)
      plt.imshow(x_train[i].reshape(28, 28))
      plt.gray()
      ax.get_xaxis().set_visible(False)
      ax.get_yaxis().set_visible(False)

# 自己符号化した画像
ax = plt.subplot(2, n, i + 1 + n)
encoded_img = np.dot(x_train[i].reshape(-1, 784), w_enc_p) + b_enc_p
decoded_img = np.dot(encoded_img.reshape(-1, 100), w_dec_p) + b_dec_p

plt.imshow(decoded_img.reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)

結果を見ると、入力に対して自己符号化後の出力がぼやけたものとして表現されています。これは、784次元だった入力を100次元に削減して表現したためになります。(岡谷先生の本によると、これは784次元のデータを固有値の大きい順に100個固有ベクトルを抽出して表現した主成分分析と同じようです) 自己符号化器は、このようにデータの特徴を取り出せるように入力データを変換する役割がありそうです。

事前学習の実装とその結果

次に上記で説明した自己符号化器を用いて事前学習を行います。 今回は自己符号化器を組み合わせた積層自己符号化器を用いて行います。 積層自己符号化器では、以下のステップに従って自己符号化器を学習し、事前学習を行います。

1. 多層のネットワークを複数の単層のネットワークに分割する
2. もっとも入力に近い単層ネットワークで自己符号化器を作成し、重み [latex]W^\left(2\right)[/latex]を得る
3. 学習した重み [latex]W^\left(2\right)[/latex] をセットし、出力層の表現 [latex]z^\left(2\right){n}[/latex]を得る
4. [latex]z^\left(2\right){n}[/latex] を入力として、次の単層ネットワークで自己符号化器を作成、重み [latex]W^\left(3\right)[/latex] を得る
5. 層の数だけ、(3), (4)を上位層に向けて繰り返す
6. 学習した重みを元のネットワークにセットし、出力層を含む上位層に新たな層を1層以上追加、その重みはランダムに初期化したうえで目標とする教師あり学習を実行する

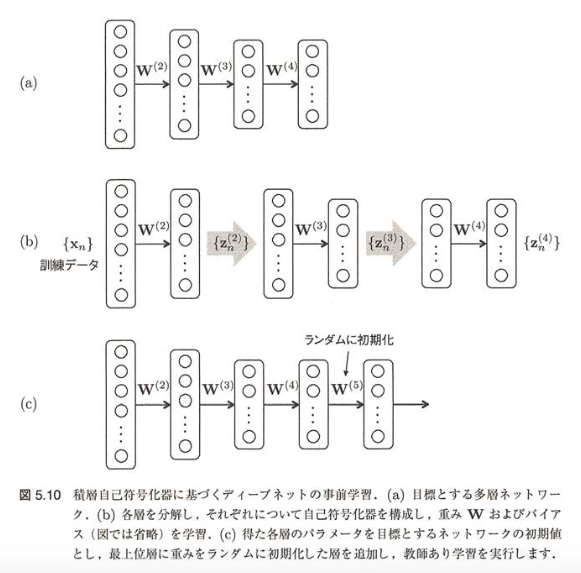
(1)~(5)の単層ネットワークでの自己符号化器の実行例は以下になります 今回は、以下のようなユニット数をもつ6層の多層ネットワークでMNISTの学習を例にして行います。

# 入力層のユニット数 = 784
# 最初の中間層のユニット数 = 100 # 2つめの中間層のユニット数 = 50 # 3つめの中間層のユニット数 = 25 # 4つめの中間層のユニット数 = 12 # 5つめの中間層のユニット数 = 5 # 6つめの中間層のユニット数 = 5 num_units1 = 100
num_units2 = 50
num_units3 = 25
num_units4 = 12
num_units5 = 5
num_units6 = 5
# 自己符号化関数
def auto_encoding(x, w_enc, b_enc, w_dec, b_dec):
      encoded = tf.nn.relu(tf.matmul(x, w_enc) + b_enc)
      decoded = tf.matmul(encoded, w_dec) + b_dec
      return decoded

x = tf.placeholder(tf.float32, [None, 784])

w_enc = tf.Variable(tf.random_normal([784, num_units1], stddev=0.01))
b_enc = tf.Variable(tf.zeros([num_units1]))

w_dec = tf.Variable(tf.random_normal([num_units1, 784], stddev=0.01))
b_dec = tf.Variable(tf.zeros([784]))

# 初回の自己符号化器の誤差関数
decoded = auto_encoding(x, w_enc, b_enc, w_dec, b_dec)

loss = tf.reduce_sum(tf.square(x - decoded))
train_step = tf.train.AdamOptimizer().minimize(loss)
sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())

i=0
for _ in range(3000):
      i += 1
      batch_xs, batch_ts = mnist.train.next_batch(100)
      sess.run(train_step, feed_dict={x: batch_xs})
      if i % 100 == 0:
          loss_val = sess.run(loss,
              feed_dict={x:mnist.train.images})
          print ('Step: %d, Loss: %f'% (i, loss_val))
# 学習した重み
w_dec_p, b_dec_p, w_enc_p, b_enc_p = sess.run([w_dec, b_dec, w_enc, b_enc])

以下長くなるので省略しますが、6層分自己符号化器を使って重みの初期値を学習していきます。 2層目では、1層目の出力を入力として使用するので自己符号化器の部分は以下のようになります。

second_x = tf.nn.relu(tf.matmul(x, w_enc_p) + b_enc_p)
decoded = auto_encoding(second_x, w2_enc, b2_enc, w2_dec, b2_dec)

最後に、(6) 学習した重みを元の多層ネットワークにセットし、本来解くべき多層ネットワークの教師あり学習を行います。

# 事前学習した重みを使ってのMNIST分類精度
x = tf.placeholder(tf.float32, [None, 784])

w1_n = tf.Variable(w_enc_p)
b1_n = tf.Variable(b_enc_p)
hidden1 = tf.nn.relu(tf.matmul(x, w1_n) + b1_n)

w2_n = tf.Variable(w2_enc_p)
b2_n = tf.Variable(b2_enc_p)
hidden2 = tf.nn.relu(tf.matmul(hidden1, w2_n) + b2_n)

w3_n = tf.Variable(w3_enc_p)
b3_n = tf.Variable(b3_enc_p)
hidden3 = tf.nn.relu(tf.matmul(hidden2, w3_n) + b3_n)

w4_n = tf.Variable(w4_enc_p)
b4_n = tf.Variable(b4_enc_p)
hidden4 = tf.nn.relu(tf.matmul(hidden3, w4_n) + b4_n)

w5_n = tf.Variable(w5_enc_p)
b5_n = tf.Variable(b5_enc_p)
hidden5 = tf.nn.relu(tf.matmul(hidden4, w5_n) + b5_n)

w6_n = tf.Variable(w6_enc_p)
b6_n = tf.Variable(b6_enc_p)
hidden6 = tf.nn.relu(tf.matmul(hidden5, w6_n) + b6_n)

# 一番上位にランダムに初期化した重みの層をつける
w0_n = tf.Variable(tf.random_normal([num_units6, 10], stddev=0.01)) b0_n = tf.Variable(tf.random_normal([10]))
p = tf.nn.softmax(tf.matmul(hidden6, w0_n) + b0_n)

# 誤差関数の設定と学習
t = tf.placeholder(tf.float32, [None, 10])

loss = -tf.reduce_sum(t * tf.log(tf.clip_by_value(p,1e-10,1.0)))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
correct_prediction = tf.equal(tf.argmax(p, 1), tf.argmax(t, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())

# 30,000 step実行
i=0
accuracy_list_stacked = []
index_list = []
for _ in range(30000):
    i += 1
    batch_xs, batch_ts = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, t: batch_ts})
    if i % 100 == 0:
        loss_val, acc_val = sess.run([loss, accuracy],
            feed_dict={x:mnist.test.images, t: mnist.test.labels})
        print ('Step: %d, Loss: %f, Accuracy: %f'
               % (i, loss_val, acc_val))
        accuracy_list_stacked.append(acc_val)
        index_list.append(i)

事前学習を使わずに通常の方法で学習したネットワークと、事前学習を使って学習したネットワークのstep数ごとの精度の変化を見てみます。

# 通常のネットワークと事前学習ネットワークの精度比較
plt.figure(figsize=(10,5))
plt.xlabel('times (* 100)')
plt.ylabel('accuracy')

plt.plot(accuracy_list, linewidth=1, color="red", label="normal")
plt.plot(accuracy_list_stacked, linewidth=1, color="blue", label="pretrained")
plt.legend(loc="lower right")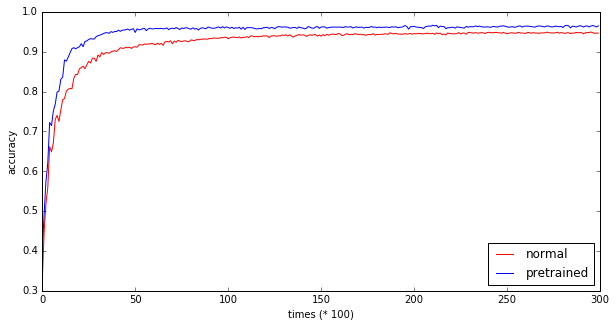

30,000 step実行時点での精度は事前学習版96.4%、通常版94.6%で通常よりも2%弱上がっています。また事前学習版の方が、重みが最適値に収束していく進み具合が通常版よりも速いように見えます (事前学習の方は2000回ほどで精度90%に到達するが、通常版は4000回まで実行しないと90%の精度に到達しない) なぜこのような事前学習が効果があるのかについては、謎な部分も多いのですが(岡谷先生本でも「もっぱら経験的な知見とい うべきであり、なぜそうなるかは理論的には解明されていません」となっていました)、 自己符号化器によって、入力データの 特徴をよりうまく捉えられていることが関係しているようです。

まとめ

実装してみることで、事前学習の効果を感じることができました。

参考文献

• 深層学習(岡谷氏著，講談社 機械学習プロフェッショナルシリーズ)
• TensorFlowで学ぶディープラーニング入門~畳み込みニューラルネットワーク徹底解説 (中井氏著, マイナビ)